Study of Self-Purification Capacity in the Semi- Arid Zones: Case of Wadi Cheliff, (Northern Algeria)
Mokadem Maamar1 * , Achour Djillali2 and Cherif El Amine1
1
Department of Hydraulics,
University of Sciences and Technology MB of Oran P.O. Box 1505,
El-Mnaouer,Oran,
31000
Algeria
2
University of Hassiba Ben Bouali,
P.O. Box 151 Hay Es-Salem, Chlef,
02000
Algeria
DOI: http://dx.doi.org/10.12944/CWE.9.3.05
The aim of this paper was to study and predict the self-purification capacity of wadi Cheliff (in the section Oum Drou –Chlef). This was done primarily by measuring the Dissolved Oxygen (DO) downstream of a pre-selected pollution discharge point on wadi Cheliff and then predicting the same using the modified Streeter-Phelps equations. Twelve sampling stations are chosen, on a section of approximately 8.5 km of the wadi Cheliff (Oum Drou - Chlef), to collect data with knowing the Biochemical Oxygen Demand (BOD), pH, stream velocity, stream depth and distance. Predicted DO deficit trend lines were first fitted by retaining the original re-aeration coefficient component, k2, of the modified Streeter-Phelps equation (United States Geological Survey equation) and subsequently by substituting it with our reaeration coefficient model. It was found that the latter displayed better predictive capacity. Results also demonstrated that the self-purification capacity of the river which is already limited by the relatively low DO saturation level is further threatened by the wastes being discharged into it at varying intervals. Some of these wastes are non-biodegradable which slows down the self-purification processes of the wadi. To preserve the underground layers of the area and to ensure a water of good quality for the irrigation, the Wadi Cheliff must be, necessarily, to protect from any pollution.
Copy the following to cite this article:
Maamar M, Djillali A, Amine C. E. Study of Self- Purification Capacity in the Semi- Arid Zones: Case of Wadi Cheliff, (Northern Algeria). Curr World Environ 2014;9 (3) DOI:http://dx.doi.org/10.12944/CWE.9.3.05
Copy the following to cite this URL:
Maamar M, Djillali A, Amine C. E. Study of Self- Purification Capacity in the Semi- Arid Zones: Case of Wadi Cheliff, (Northern Algeria). Curr World Environ 2014;9(3). Available from:http://www.cwejournal.org/?p=7500
Download article (pdf) Citation Manager Publish History
Select type of program for download
| Endnote EndNote format (Mac & Win) | |
| Reference Manager Ris format (Win only) | |
| Procite Ris format (Win only) | |
| Medlars Format | |
| RefWorks Format RefWorks format (Mac & Win) | |
| BibTex Format BibTex format (Mac & Win) |
Article Publishing History
| Received: | 2014-09-10 |
|---|---|
| Accepted: | 2014-10-23 |
Introduction
Water quality modeling has been shown to be a useful tool in strategic water quality management (Fan et al. 2009). The literature contains very few studies on the water quality modeling for small rivers, and such studies as have been published are fairly limited in scope (Giorgio M., Gaspare V. 2010) and especially for the arid and semi-arid areas.
The aim of models self-purification is predict, at the space-time forecast, the effects of an organic matter rejection on the dissolved oxygen content of the receiving medium, by taking account of its characteristics and those of the rejection. Progressively of progress of the scientific research, the models were become more complex by integrating a growing number of factors like dilution, sedimentation, adsorption, dispersion, the advection and of the re-aeration of the atmosphere (Fischer et al. 1979; Koussis 1983; Koussis et al. 1983, 1990; McBride and Rutherford 1984). at the same time one increased, on the one hand, the difficulties of using them in practice (Snowling and Kramer 2001) and on the other hand the error between simulations and the total sensitivity of the model increases and consequently the most complex model is not necessarily the most “useful” (Lindenschmidt 2006).
Reliable model calibration requires an extensive array of water quality data that are generally rare and resource-intensive, both economically and in terms of human resources, to collect (Mannina and Viviani 2010).
The conventional method for the analysis of the water pollution is based on the equation of Streeter-Phelps (Streeter and Phelps 1925, 1936; Cox 2003; Lin and Lee 2007; Omole and Longe 2012; Omole et al. 2012) this model does not introduce the decantable component of the DBO (Tyagi et al. 1999). Bhargava considered that the DBO includes/understands a decantable part and another dissolved (Bhargava 1983; Velz and Gannon 1962) added a factor to the constant of DBO rate, k1, exponential form of kinetics of first order to explain the reduction in DBO by the phenomenon of sedimentation.
Thomann and Mueller (1987) carried out an important modification in the model of Streeter and Phelps, by the separation of DBO in two carbonaceous and nitrogenized components because these two elements have a rate of different deoxygenation and reaeration. However oxygen dissolves remainder the same one, it is supplemented with a dependence of the temperature.
In Algeria, the water resources of surface are very limited and difficult to exploit, this is why any risk of contamination or of pollution deserves to be underscored, forwarded and modeled.
The wadi Cheliff, one of the most important rivers in Algeria, par excellence constitutes a vector of pollution for the underground layers and the irrigation. To know the quality of this water is essential for the management of this resource and its environment.
The wadi Cheliff is a concrete example of the width of a pollution of any kind to knowing physical, chemical and bacteriological following the excessive rejections of urban or industrial nature which it receives with the length of the year without any preliminary treatment. Thirty-two (32) production units are established in the watershed of the wadi Cheliff and generate a pollution of about 410.000 population equivalents (ABHCZ 2005).
The model considered here for the first time is a simulation of the Oxygen dissolved in the courses in Algeria. A comparison between this model and the linear model of Streeter and Phelps will be carried out on a section of the Wadi Cheliff.
Study Area
The watershed of Cheliff occupies a surface of 47.269 km2. It extends between the meridian lines 0° and 3°30' Eastern and between the latitudes 34° and 36° Northern. It covers four under watersheds: Cheliff upstream of Boughezoul, the high and the middle Cheliff, Lower Cheliff, the Mina and the coastal one. It is limited to North by the Mediterranean, in the West by the Oranais watershed, the South by the high plains and the East by the of Algiers watershed (Fig. 1).
|
|
Figure 1: Watershed of wadi Cheliff |
The area is characterized by a semi-arid climate with very hot summers and cold winters (Boulaine, 1957). The considerable variation (18 °C) between the maximum temperature recorded in July (29 °C) and the minimal one in January (11 °C) a continental climate marked, in spite of the proximity of the sea; indeed, the mounts of Dahra form a barrier isolating from the watershed Cheliff of the regulating influence of the Mediterranean over a 70 km length (Bettahar et al. 2009).
Matrials and Methods
The model is applied to a section of the Wadi Cheliff length approximately 8.5 km delimited by the section upstream to the level of the town of Oum Drou until the section swallows taken on the level of the center of the town of Chlef.
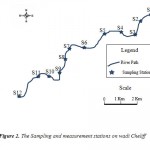
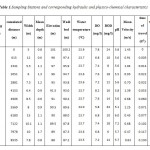
Twelve (12) sampling stations were selected on the level of this section (Fig. 2). The distance of the stations compared to the first station (Oum Drou) is defined in table 1.
The data measured on the level of these stations are the DBO5 analysis were stored in a series cooled incubator at a controlled temperature of 20°C, water velocity was measured using a reel current meter, the ambient and water temperature data were obtained using a portable conductimeter, water pH was obtained using a handheld pH-meter, the dissolved Oxygen evaluated using a portable O2-meter. The total distance of the segment and the global position of each sampling station were obtained with the Garmin Handheld GPSMAP 78S.
|
|
Figure 2: The Sampling and measurement |
Theory
The model of Streeter and Phelps (1926), for the river Ohio, described the space-time evolution of the concentration of dissolved oxygen and BOD to the downstream after pollution discharges, was proposed:
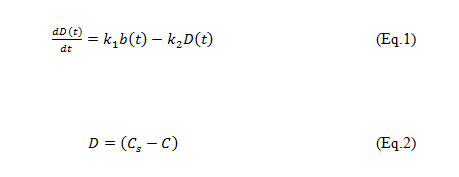
Where, D = Dissolved Oxygen deficit, b = Ultimate first stage BOD of mix at the point of discharge in mg/l, k1 = deoxygenation coefficient, k2 = re-aeration coefficient, t = time in days, C = concentration of OD, Cs = concentration of saturation of DO.
The model uses the coefficients k1 and k2 which is dependent respectively on the waste characteristics alone while the re-aeration coefficient k2, is dependent on such factors as water temperature, velocity and depth of the river.
The equation 1, after integration (Waite et al. 1977; Kiely 1998; Longe and Omole 2008) gives:
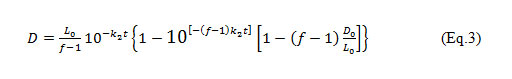
Where: D = the predicted DO deficit in mg/l after time t; L0 = Ultimate first stage BOD of mix at the point of discharge in mg/l; D0 = Initial DO deficit of the mix at the mixing point in mg/l; k1= De-oxygenation coefficient for the effluent; k2=Re-aeration coefficient for the stream; t = time.

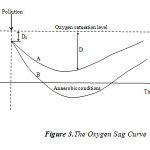
The variation of the dissolved oxygen deficit D is described by a curve spoon shaped (Fig. 3) which can be interpreted as follows: With the starting point, and before the pollution discharges, water is rich in oxygen; the dissolved oxygen deficit is low. After the introduction of waste water, a biochemical decomposition of this last with dissolved oxygen starts according to the equation N°1. A dissolved oxygen deficit is established and increases gradually. This dissolved oxygen deficit, will be at least filled by the reaeration of water by gas transfer. After a certain distance (time), water in the stream, including waste water, is again saturated or almost with dissolved oxygen, C ≈ Cs (Curve A). Curve B presents a case where the pollution leads to the river becoming septic (Anaerobic).
The concentration of saturation out of oxygen Cs in water is calculated, according to the temperature T, the formula empirical (Fair et al. 1968; Bowie et al. 1985) following is used
Cs = 14.64 - 0.41. T + 0.008. T2 (Eq.5)
The coefficient of reaeration k2 is determined by the following relation (Metcalf 1972)

Where, h = depth of the river in m, v = velocity of the river in m/s, α, n, m = empirical coefficients.
|
|
Figure 3: The Oxygen Sag Curve |
Results and Discussions
Just before the rejection of the waste water (S1), the water of the wadi is rich in dissolved oxygen with a value of 7.7 mg/l which is very close to the saturated dissolved oxygen, at this period of the year, level of 8.4 mg/l correspondent at a temperature of approximately 24°C. This concentration, which is highest of the values measured in the sampling stations, starts to decrease up to a minimal value of 6.2 mg/l (S3). At this place relatively high speed (1.04 m/s) to support a good reaeration and consequently good self-purification and the OD take a value of 7.5 mg/l (S4).
The section between S5 and S6 is characterized by low slopes (0.6 to 3 ‰) which generate low velocity of flow (thus a relatively high time of travel) which favor the oxygen consumption by the bacterial activity. It takes a value of 7.1 mg/l to start to increase up to the value of 7.6 mg/l (S7). This increase is stopped by a rejection of waste water without treatment of the agglomeration of Chega and the cycle of the process of biological breakdown repeats i.e. a reduction in the OD (6.7 mg/l at the S9 station) then an increase (7.5 mg/l at the S10 station). Another rejection of waste water (of the Eastern part of Chlef) comes to stop, again, the phenomenon of the self-purification of the wadi Cheliff and the OD decreases up to the value of 6.8 mg/l.
It remains to be announced that the pH of the water of the wadi Cheliff is slightly acid, its median value is of 5.77 this is due to the bio-degradation of part of the organic matters in anaerobic medium especially in the dry season.
From this a k2 model for Wadi Cheliff is calculated from experimental results using Eq. (7)
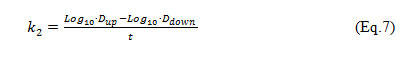
Where, Dup= initial DO deficit at the upstream; Ddown= DO deficit at any downstream point; t = time of travel between two points successive.
|
|
Table 1: Sampling Stations and corresponding |
To find the relationship between the calculated values of k2a non-linear regression analysis could be used, the stream velocity and stream depth by obtaining the constants of the relationship which are also known as the coefficients of regression β1, β2, β3 using Eq. (8)

Where, V = stream flow velocity, in meters per second and H = Hydraulic Radius, in meters.
The k2 model for wadi Cheliff (Eq. 9) was developed while determining the parameters β1, β2 and β3. These parameters are the unknown values of the function that must be determined. Since β2 and β3 are in a non-linear position with respect to the defined relationships, a non-linear regression was done to determine the parameters.
Following the calibration of the model is obtained by plotting the dispersion plot of k2 (measured) and k2 (computed), and the non-linear regression analysis of data using the Mathcad software
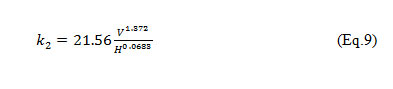
Following the non-linear regression analysis, the model output passed with the following statistics: Error Sum of Squares, SSE = 8.561; Coefficient of determination, R2 = 0.942; and a Root Mean Square Error, RMSE = 1.723.
The re-aeration coefficient proposed by Streeter et al.(1936) is defined thus

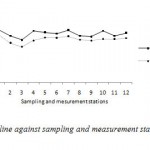
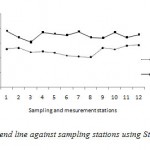
By substituting equation 9 into equation 3, the broken curve in Figure 4 was obtained. However, when the equation 3 was used with the re-aeration coefficient proposed by Streeter et al.(1936) (Eq. 10), the predicted DO deficit curve that was obtained is presented in Figure 5.
|
|
Figure 4: DO deficit trend line against sampling |
|
|
Figure 5: DO deficit trend line against sampling |
Furthermore the plot of DO along the path of the wadi (Fig. 4) displayed a marked difference from the expected normal spoon-shaped DO curve (Fig. 3). The DO curve along wadi Cheliff displayed sinusoidal tendencies which suggest that the progressive recovery process was being interrupted at several intervals in the section.
By comparing the results of these deficits of dissolved oxygen simulated by the model suggested of the wadi Cheliff, the Streeter-Phelps model and measurements of the analysis, one notes: the results of the model suggested approach those measured better that those provided by the model Streeter - Phelps.
Conclusion
After this study; we can say that the Wadi Cheliff has a capacity normal but limited to purify itself from many pollutants mainly the rejections of domestic or industrial waste water (agro-alimentary) especially in the dry season; on the one hand the flow is low generating low velocity of flow; on the other hand the temperature, during this time of the year, exceeds the 29°C what decreases the solubility of the OD (crucial factor to the bio-degradation of the organic matters) in water. The DO curve along wadi Cheliff displayed sinusoidal tendencies which suggest that the wadi self-purification processes are being interrupted at several intervals in the section.
The development and validation of Cheliff model has been carried out; This model is suggested to study the quality of the wadi Cheliff and its capacity of self-purification requires, for its application, only knowledge that hydraulic properties of the wadi and characteristics physico-chemical of water, this is very important and useful especially for developing countries which miss data, means and/or of management; this to be used like a tool of forecast and assistance for management such as the designation of the zones of intake of water for the irrigation and the knowledge of the quality of water of the wadi in every point of the section. This forecast makes it possible to each time avoid the recourse to expensive analyzes. Cheliff model is therefore recommended for application in future reaeration studies on wadi Cheliff.
To Safeguard the public health and to protect the groundwater of pollution transported by the wadi Cheliff require measurements to improve the capacity of self-purification of this last. Among these measurements, the construction of the waste water purification plants for the waterside agglomerations; to activate the “police force of water” so that the regulations of environmental protection are respected.
References
2. Bettahar, N. ; Benamara, A. ; Kettab, A. ; Douaoui, A. Risque de pollution nitratée des zones semi-arides : cas de la vallée du moyen Cheliff occidental (Nord Algérien).Journal of Water Science, 22 (1), 69–78 (2009).
3. Bhargava, D. Most rapid BOD assimilation in Ganga and Yamuna rivers. Journal of Environmental Engineering.ASCE, 109; 174–187 (1983).
4. Boulaine, J. Etude des sols des plaines du Chéliff ; Thèse d’Etat de l’université d’Alger :Alger (1957).
5. Bowie, G. et al. Rates.Constants, and Kinetic Formulations in Surface Water Quality Modelling. US Environmental Protection Agency.Athens, Georgia, USA (1985).
6. Cox, B. A review of dissolved oxygen modelling techniques for lowland rivers. Sci. Total Enviro (2003).
7. Fair, G.M.; J.C. Meyer; D.A. Okun. Elements of water supply and wastewater disposal,2nd Ed.;John Wiley & Sons: N.Y (1971).
8. Fan, C.;Chun, H.;Wei-Shen, W. Aninnovative modeling approach using Qual2K and HECRAS integration to assess the impact of tidal effect on River Water quality simulation. Journal of Environmental Management (2009).
9. Fischer, H.; List, E.; Koh, R.; Imberger, J.; Brooks, H. Mixing in Inland and Coastal Waters;Academic Press: New York (1979).
10. Giorgio, M.; Gaspare, V. Water quality modeling for ephemeral rivers: Model development and parameter assessment.Journal of Hydrology, 393, 186–196 (2010).
11. Kiely, G. Environmental Engineering;McGraw Hill (U.K.) Ltd (1998).
12. Koussis, A. Unified theory for flood and pollution routing.Journal of Hydraulic Engineering, ASCE 109, 1652–1663 (1983).
13. Koussis, A.; Kokitkor, P.; Mehta, A. Modelling DO condition in stream with dispersion. Journal of Environmental Engineering, ASCE 116, 601–614 (1990).
14. Koussis, A.; Saenz, M.; Tollis, I. Pollution routing in streams. Journal of Hydraulic Engineering, ASCE 109; 1636–1651 (1983).
15. Lindenschmidt, K. The effect of complexity on parameter sensitivity and model uncertainty in river water quality modeling.Ecological Modeling, 190; 72–86 (2006).
16. M e t c a l f & E d d y. W a s t e w a t e r engineering: treatment disposal reuse. McGraw-Hill:New York (1972).
17. McBride, G.; Rutherford, J. Accurate modeling of river pollutant transports.Journal of Environmental Engineering, ASCE 110; 808–826 (1984).
18. Omole, D.; Adewumi, I.; Longe, E.; Ogbiye, A. Study of Self Purification Capacity of River Atuwara in Nigeria.International Journal of Engineering and Technology; 2; 229-235 (2012).
19. Omole, D.; Longe, E. Re-aeration Coefficient Modeling: A Case Study of River Atuwara in Nigeria. Research Journal of Applied Sciences, Engineering and Technology, 4; 1237-1243 (2012).
20. Snowling, S.; Kramer, J. Evaluating modelling uncertainty for model selection. Ecological Modelling; 138(1), 17-30 (2001).
21. Streeter, H.; Phelps, H. A study of the pollution and natural purification of the Ohio river.U. S. Public Health Service,(1925) .
22. Tyagi, B.; Gakkhar, S.; Bhargava, D. Mathematical modeling of stream DO–BOD accounting for settleable BOD and periodically varying BOD source. Environmental Modeling & Software14, 461–471 (1999).
23. Velz, C.; Gannon, J. Biological extraction and accumulation in stream self-purification. 1st International Conference of Water Pollution Research, (1962).
24. Waite, T.; Freeman, N. Mathematics of Environment Processes.Lexington Books, London. (1977).