Comparative Study of Daily Rainfall Forecasting Models Using Adaptive-Neuro Fuzzy Inference System (ANFIS)
M. A. Sojitr1 * , R. C. Purohit1 and P. A. Pandya2
1
Department of Agricultural,
Junagadh Agricultural University,
Junagadh,
362001
Gujarat
India
DOI: http://dx.doi.org/10.12944/CWE.10.2.19
The study was carried out to develop rainfall forecasting Models. Adaptive Neuro-Fuzzy Inference System (ANFIS) was used for developing Models rainfall of Udaipur city. Two data sets were prepared using 35 year of weather parameters i.e. wet bulb temperature, mean temperature, relative humidity and evaporation of previous day and previous moving average week were used to prepare case I and case II respectively. Gaussian and Generalized Bell membership functions were used to prepare models. Statistical and hydrologic performance indices of ANFIS (Gaussian, 5) gave better performance among developed four models. The study showed that sensitivity analysis revealed wet bulb temperature is most sensible parameter followed by mean temperature, relative humidity and evaporation.
Copy the following to cite this article:
Sojitra M. A, Purohit R. C, Pandya P. A. Comparative Study of Daily Rainfall Forecasting Models Using Adaptive-Neuro Fuzzy Inference System (ANFIS). Curr World Environ 2015;10(2) DOI:http://dx.doi.org/10.12944/CWE.10.2.19
Copy the following to cite this URL:
Sojitra M. A, Purohit R. C, Pandya P. A. Comparative Study of Daily Rainfall Forecasting Models Using Adaptive-Neuro Fuzzy Inference System (ANFIS). Curr World Environ 2015;10(2). Available from: http://www.cwejournal.org/?p=11969
Download article (pdf)
Citation Manager
Publish History
Select type of program for download
| Endnote EndNote format (Mac & Win) | |
| Reference Manager Ris format (Win only) | |
| Procite Ris format (Win only) | |
| Medlars Format | |
| RefWorks Format RefWorks format (Mac & Win) | |
| BibTex Format BibTex format (Mac & Win) |
Article Publishing History
| Received: | 2015-04-30 |
|---|---|
| Accepted: | 2015-07-16 |
Introduction
Rain is the most important phase of hydrologic cycle and prime requirement for living organism. It comes in different forms like fog, mist, drizzle, snow, sleet and glaze. The rain water in the form of soil moisture and groundwater are the most important requirements for agricultural production and social development in country like India where 68 per cent of total geographical are comes under the rainfed condition. India has adequate quantity water but uneven spatial distribution of rainfall has made to face flood and drought condition some parts of Country. The strong link has been observed in the past between country’s Gross Domestic Product (GDP) and year to year variations of rainfall. India receives 75 per cent rainfall through Southwest monsoon wind due to generation of law pressure in arabian sea and bay of Bengal. The Indian summer monsoon is spread over four months and it duration varies 75 to 120 days western Rajasthan and southern western region of country. Its spatial distribution varies from 500 mm to 3798 mm in western Rajasthan to coastal area of Karnataka (Amarsinghe and Shrama,1 2009). Guhathakurta and Rajeevan2 (2006) observed the decreasing trend for 17 sub-divisions in Contribution of month June, July and September rainfall to annual rainfall and increasing trend was found for August rainfall in 19 other subdivisions.
There is great task has been carried out by world wise meteorological organization for weather forecasting for their respective area. Adaptive Neuro Fuzzy Inference System (ANFIS) is Takagi–Sugeno fuzzy based inference system. It works on integration of neural networks and fuzzy logic principles and has advantage of both of them. Tektas3 (2010) applied ANFIS and ARIMA models for forecasting of Goztepe, Istanbul, Turkey. Changsam4 (2012) developed ANFIS models for monthly precipitation using 30 sets of meteorological variable. Jesada et al.5 (2012) used Modular Fuzzy Inference System (Mod FIS) to forecast monthly rainfall data in the northeast region of Thailand. Adaptive Neuro-Fuzzy Inference System (ANFIS) and Autoregressive Moving Average (ARIMA) models were developed by Suthartono et al.6 (2012) to forecast monthly rainfall at Pujon and Wagir in Indonesia. Past research shows that ANFIS performs better than Statistical and ANN models. Dostarani et al.7 (2010) assessed the applicability of ANFIS and ANN for predicting the rainfall and found that both ANN and ANFIS models are efficient tool to model and predict precipitation amounts 12 months in advance. El-Shafie et al8 (2011) has proposed to forecast the rainfall for Klang river in Malaysia on monthly basis. Chien-Lin Huang et. al9 (2014) constructed a typhoon precipitation forecast model which has forecasted rainfall one to six hours in advance using optimal model parameters and structures retrieved from a combination of the adaptive network-based fuzzy inference system (ANFIS). Fi-John Chang et al.10 (2014) stated that assimilated precipitation gave reliable and stable rainfall forecasts with the correlation coefficients higher than 0.85 and 0.72 for one- and two-hour-ahead rainfall forecasting, respectively. The present study will be useful to be prepared for problems regarding scarcity and drainage of rainfall for the Udaipur city and also to farming community for decision making regarding sowing of crops.
Materials and Methods
Study Area
Udaipur city of Rajasthan, India is situated at 24°58' N latitude and 73°68' E longitude with elevation 598 m above the mean sea level. It has tropical semiarid climate with an average annual rainfall of 617mm (1979-2013) and average annual pan evaporation 5.1 mm/day (2002-12). May is the hottest month with mean monthly maximum temperature 39.8°C (2002-12) and January is the coolest month with mean monthly minimum temperature 4.9°C (2002-2012). Highest mean monthly pan evaporation shows in the month of July 10.6 mm/day (2002-2012).
Data acquisition and pre analysis
The rainfall amount and its distribution in the temporal and spatial dimensions depends on many variables, such pressure, temperature, and wind speed and direction (luk et al.11 2001). The Rainfall, Evaporation, Relative Humidity, Wind Velocity, Wet bulb, Dry bulb Temperature and Mean Temperature data were collected for the study. The data for the period of May 25th to October 30th for the year 1979 to 2013 were subjected to pre-analysis and formulation of the data base. Thus the total number of data for each year’s period were 153. Data from 1979-2008 were used formulate and validate and data from 2009-13 were used forecasting and checking the error.
Fuzzy Logic Systems
Fuzzy sets
Fuzzy sets are used in fuzzy logic. In classical set theory the membership of elements, in relation to a set, is determined in binary terms according to a crisp condition – an element either belongs or does not belong to the set. The gradual assessment of the membership function is permitted by fuzzy set theory. A membership function may act as an indicator function, mapping all elements to either 1 or 0 for a certain universe, as in the classical notion. Therefore, Fuzzy sets can be used as an extension of classical set theory.
Adaptive Neuro-Fuzzy Inference System (ANFIS) model
ANFIS is a Takagi-Sugeno-kang (TSK) fuzzy based fuzzy mapping algorithm. ANFIS is a hybrid fuzzy system in which the fuzzy system is arranged in parallel fashion based on competitive or co-operative relationship. Five primarily components as: inputs and output data base, a Fuzzy system generator, a fuzzy inference system and an adaptive neural network are included in a conceptual ANFIS. The Fuzzy inference systems t which are used for mapping in this model are Input characteristics to input membership functions,2 Input membership functions to rules,3 Rules to a set of output characteristics.4 Output characteristics to output membership function.5 The output membership function to a single valued output, or a decision associated with the output. The neuro adaptive learning technique gives fuzzy modeling method to obtain information about a data set to work out the membership function parameters which best allow the associated fuzzy inference system to get the given input/output data. No systematic procedure to define the membership function parameters is available in fuzzy logic. The definition of premises and consequence as fuzzy sets is required for construction of Fuzzy rule. An Artificial Neural Network (ANN) is capable of learning from input and output pairs and adapt to it in an interactive manner. The basic problem in fuzzy system design, defining the membership function parameters and design of fuzzy if-then rules is eliminated by ANFIS by using the learning capability of ANN for automatic fuzzy rule generation and parameter optimization effectively. There are two types of FIS, Mamdani FIS and Sugeno-Takagi FIS. These two systems differ from each other in terms of definitions of the consequence parameter. The consequence parameter in Sugeno FIS is either a liner equation, called “first order Sugeno FIS”, or constant coefficient, “zero-order Sugeno FIS”. The Sugeno-type FIS,used in this study is a combination of a FIS and an adaptive neural network. The hybrid learning algorithm is used as an optimization method for membership function parameter training. The hybrid method is a combination of least squares estimation with back propagation gradient descent method.
ANFIS architecture
ANFIS is an adaptive network functionally equivalent to fuzzy inference system, known as “Adaptive Neuro-Fuzzy Inference System”. The Takagi-Sugeno type fuzzy inference system is used in ANFIS. The linear combination of input variables plus a constant term will be the output of each rule. The weighted average of each rule’s output is final output. Basic ANFIS architecture given in fig. 1 that has two inputs X and Y and one output f is shown in fig. 2. Two Takagi-Sugeno if-then rules are contained in the rule base as given below
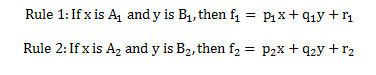
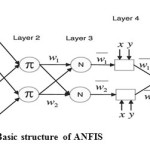 |
Figure 1: Basic structure of ANFIS Click here to View figure |
 |
Figure 2: A two input first order Sugeno-fuzzy model Click here to View figure |
The node functions in the same layer are described below:
Layer 1: Every node I in this layer is a square node with a node function as.
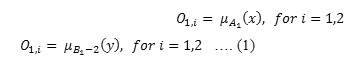
Where x is the input to node i, and i A (or i−2 B) is a linguistic label (such as “small” or “large”) associated with this node. In other words, O1,i is the membership grade of a fuzzy set A and it specifies the degree to which the given input x satisfies the quantifier A . The membership function for A can be any appropriate membership function, such as the Triangular or Gaussian. When the parameters of membership function changes, chosen membership function varies accordingly, thus exhibiting various forms of membership functions for a fuzzy set A . Parameters in this layer are referred to as “premise parameters”.
Layer 2: Every node in this layer is a fixed node labeled as II, whose output is the product of all incoming signals.
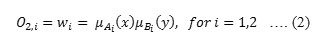
The firing strength of a fuzzy rule is represented by each node
Layer 3: Every node in this layer is a fixed node labeled N. The ratio of the rule’s firing strength of the sum of all rule’s firing strengths is calculated by the ith node.
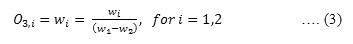
This layer gives out put which are called “normalized firing strengths”.
Layer 4: Every node i in this layer is an adaptive node with a node function as.
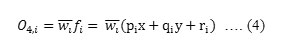
where,W-tis is a normalized firing strength from layer 3 and {pi, qi, ri}is the parameter set of this node. Parameters in this layer are called “consequent parameters”.
Layer 5: The single node in this layer is a fixed node labeled Σ, the overall output as the summation of all incoming signals is computed by this node.
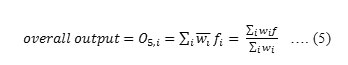
This layer is called as the output nodes in which the single node computes the overall output by summing all the incoming signals and is the last step of the ANFIS. Thus, the network fed the input vector layer by layer.
Development of ANFIS model
Four weather parameters Wet bulb Temperature, Mean Temperature, Relative Humidity and Evaporation of previous day and previous moving average week were taken as input parameter for Case I and Case II respectively. The present day rainfall is output for both the case. Four models of ANFIS were generated for Case I and Case II. Let the observed values of Wet bulb Temperature, Mean Temperature, Relative Humidity and Evaporation represented as Twi,j, Ti,j, RHi,j, and Ei,j respectively for jthday of the ith year (i = 1,2,….,M and j = 1,2,…,N).
The functional form of the models can be given as
Pi,j = f(TWi,j-1, Ti,j-1, RHi,j-1, Ei,j-1) .....................(6)
Sensitivity Analysis
Sensitivity analysis was carried out for ANFIS (Gaussian, 5) to determined most and less sensible weather parameter for rainfall forecasting by adding and removing weather parameter one by one. It was followed by formulation and validation of models. Statistical indices used to sensitivity analysis of models.
Performance and Evaluation of Models
Visual observation was used for performance evaluations of the models based on the graphical comparison between desire and predicted values of rainfall. Statistical and hydrological indices were also determined for testing the goodness of fit for comparison between desire and predicted values of rainfall.
Results and Discussion
Results and Discussion is presented for the comparative study rainfall forecasting models and sensitivity analysis for ANFIS (Gaussian, 5) of best suited models.
Comparative Study of ANFIS Models formulation
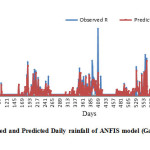
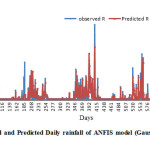
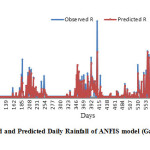
Gausian,2, Generalised bell,4, Gaussian,5 and Generalised bell, 3 models were formulated for Case I and Case II respectively. Visual observation was carried out for quantitative performance as shown in fig.3 to fig 7 respective models for testing year from 2009 to 2013. It can be observed from fig. 3 to fig. 7 that models showed closeness between Observed and Predicted value of Rainfall.
 |
|
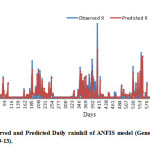 |
Figure 4: Observed and Predicted Daily rainfall of ANFIS model (Generalised bell,4) during testing period (2009-13). Click here to View figure |
 |
|
 |
|
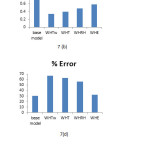 |
Figure 7: Performance of Sensitivity analysis for ANFIS (Gaussian, 5). Click here to View figure |
Different Statistical indices like Correlation Coefficient (CC), Mean Square Error (MSE), Normalise Mean Square Error (NMSE), Percent Error (% error) and hydrologic indices like Volumetric Error (EV) and Coefficient Efficiency (CE) were calculated of Case I and Case II for training and testing respectively as depicted in Table 1. The results revealed that Gaussian, 2 performed better than Generalised bell, 4 for Case I and Gaussian, 5 performed better than Generalised bell, 2 for case II. The overall results indicate that Gaussian membership function performed better than Generalised bell. It can be seen from table that ANFIS models (Gaussian, 5) perform better among four models with CC, MSE, AIC, % Error, CE, EV as 0.002, 0.36, 0.87, -4674, 30.27, 82.30, 8.75 respectively. Correlation Coefficient (CC) indicates correlation between desire and predicted value of rainfall. Other statistical indices also indicate ANFIS (Gaussian, 5) performed better among four selected models. ANFIS models Gaussian, 5, and Generalised bell, 2 of Case II performed better than Gaussian, 2 and Generalised Bell, 4 of Case I, so it clearly indicates way of prepared data set also play important role for formulation of the models and rainfall forecasting depends on long term weather.
Table 1: Performance Evaluation of Anfis Models During Training and Testing Period
|
Performance indices |
Case I (One day lag) |
Case II (Moving average week) |
||||||
|
Training |
Testing |
Training |
Testing |
|||||
|
Gauss, 2 |
G- bell, 4 |
Gauss, 2 |
G - bell, 4 |
Gauss, 5 |
G - bell, 2 |
Gauss, 5 |
G - bell, 2 |
|
|
MSE |
0.009 |
0.007 |
0.005 |
0.004 |
0.004 |
0.005 |
0.002 |
0.002 |
|
NMSE |
0.75 |
0.72 |
0.59 |
0.64 |
0.40 |
0.44 |
0.36 |
0.38 |
|
CC |
0.86 |
0.88 |
0.83 |
0.80 |
0.90 |
0.89 |
0.87 |
0.86 |
|
AIC |
-31704 |
-31678 |
-4978 |
-4704 |
-32076 |
-31412 |
-4674 |
-4452 |
|
% Error |
45.27 |
60.85 |
40.85 |
38.12 |
32.14 |
40.28 |
30.27 |
37.42 |
|
CE |
85.48 |
86.48 |
82.30 |
79.66 |
83.80 |
85.34 |
82.30 |
79.66 |
|
EV |
15.04 |
10.28 |
8.28 |
9.65 |
21.24 |
22.19 |
8.75 |
12.85 |
(G- bell: Generalised Bell, Gauss: Gaussian)
Sensitivity Performance
Sensitivity analysis helps to determine sensitivity of responsible weather parameters for development of rainfall forecasting models. Different statistical indices like CC, MSE, NMSE, % Error and AIC value were analyzed and results are given in presented in Fig. 7. It is clearly observed from fig. 7 that wet bulb temperature is the most sensible weather parameter for formulating rainfall forecasting models followed by mean temperature, relative humidity and evaporation.
There were several ANFIS models formulation for rainfall forecasting of Udaipur city, Rajasthan, India. Gaussian and Generalized bell membership function performed equally for development nonlinear relationship. Here ANFIS (Gaussian, 5) gave best results for Udaipur city within all acceptable limits of statistical indices.
References
- Amarsinghe, U. and Sharma, B. Water PS Productivity of Food Grains in India: Exploring Potential Improvements. Strategic Analysis of National River Linking Project (NRLP) of India, 4:13-54, (2009).
- Guhathakurta, P. and Rajeevan, M. Trends in the rainfall pattern over India, NCC Research Report National Climate Centre Office of the Additional Director General of Meteorology (Research), Indian Meteorological Department, (2006).
- Tektas, M. Weather Forecasting Using ANFIS and ARIMA Models. Environmental Research, Engineering and Manage ment. 51:5-10, (2010).
- Changsam J., Ju-Young S., Taesoon K. and Jun-Haneg H. Monthly Precipitation Forecasting with a Neuro-Fuzzy Model. Water Resources Management, 26:4467-4483, (2012).
- Jesada K., KokWai W. and Chun Che F. Rainfall Prediction in the Northeast Region of Thailand using Modular Fuzzy Inference System, IEEE World Congress on Computational Intelligence, 10-15, (2012).
- Suthartono, Faulina R., Lusia, D.A., Otok, B.W., Sutikno, Kuswanto, H., Ensemble method based on ANFIS-ARIMA for rainfall prediction. Statistics in Science, Business, and Engineering (ICSSBE), International Conference, 978-1-4673-1581-4, (2012).
- Dastorani, M. T., Moghadamnia, A., Piri, J. and Rico-Ramirez, M. Application of ANN and ANFIS models for reconstructing missing flow data. Environmental Monitoring Assessment,166 :421-434, (2010).
- El-Shafie A., Jaafer O. and Seyed A. Adaptive neuro-fuzzy inference system based model for rainfall forecasting in Klang River, Malaysia, International Journal of the Physical Sciences, 6(12): 2875-2888, (2011).
- Chien-Lin Huang, Nien-Sheng Hsu, Chih-ChiangWei, and Chun-Wen L. Using Artificial Intelligence to Retrieve the Optimal Parameters and Structures of Adaptive Network-Based Fuzzy Inference System for Typhoon Precipitation Forecast Modeling, Advances in Meteorology, 2015: 1-22,( 2014).
- Fi-John Chang, Yen-Ming Chiang, Meng-Jung Tsai , Ming-Chang Shieh, Kuo-Lin Hsu, Soroosh Sorooshian. Watershed rainfall forecasting using neuro-fuzzy networks with the assimilation of multi-sensor information, Journal of Hydrology, 508: 374–384, (2014).
- Luk, K. C., Ball, J. E.and Sharma A. An application of artificial neural networks for rainfall forecasting. Mathematical and Computer Modelling, 33:883-699, (2001).






