Determination of Shadow Price of Iran Electricity Market Using the Fuzzy Electricity Generation Planning
Bahareh Hashemlou1 * , Arashk Masaeli1 , Hossein Sadeghi1 , Alireza Nasseri1 and Mohammadhadi Hajian1
1
Tarbiat Modares University,
Tehran,
Iran
DOI: http://dx.doi.org/10.12944/CWE.10.1.09
Copy the following to cite this article:
Hashemlou B, Masaeli A, Sadeghi H, Nasseri A, Hajian M. Determination of Shadow Price of Iran Electricity Market Using the Fuzzy Electricity Generation Planning. Curr World Environ 2015;10(1) DOI:http://dx.doi.org/10.12944/CWE.10.1.09
Copy the following to cite this URL:
Hashemlou B, Masaeli A, Sadeghi H, Nasseri A, Hajian M. Determination of Shadow Price of Iran Electricity Market Using the Fuzzy Electricity Generation Planning. Curr World Environ 2015;10(1). Available from: http://www.cwejournal.org/?p=8747
Download article (pdf)
Citation Manager
Publish History
Select type of program for download
| Endnote EndNote format (Mac & Win) | |
| Reference Manager Ris format (Win only) | |
| Procite Ris format (Win only) | |
| Medlars Format | |
| RefWorks Format RefWorks format (Mac & Win) | |
| BibTex Format BibTex format (Mac & Win) |
Article Publishing History
| Received: | 2015-02-12 |
|---|---|
| Accepted: | 2015-03-06 |
For both power and electricity energy levels, electricity is a market which exchanges and deals electricity in regional, national, and international levels. Power price is regarded as the main economic indicator in the market for detecting the required investments made in various sectors. To gain higher revenue profits, the investors of this sector assigning higher prices to electricity. However, by entering the investors to sectors with higher prices, the restrictions and price making policies are beyond handling. The mentioned factors coupled with the existing requirements and restrictions in power industry highlights the main role of pricing in this sector.
On the other hand, considering the importance and effect of greenhouse gas emission on climatic variations of the present century, to use underground oil resources for power generation first the price of electricity must be determined in every country. In this regard, it is necessary to make a comparison between the prices of electricity generated from oil and clean energy, so that not only the greenhouse gas emission can controlled, but also proper decisions can be made about the executive polices, legislations, and supervisions. Shadow prices are among the main sources for environmental decision making applicable in the present research. The shadow prices are divided into the technical and economic prices, where each one studies the shadow prices from different methodologies and perspective. The present study was conducted to estimate shadow prices of electrical energy in Iran’s electricity market using the models used for development of Iran’s power industry. In this regard, the second part of this paper reviews the literature of shadow price in electricity sector; part 3 explains the electricity model in Iran; part 4 explores the study method; part 5 presents the results and outputs; and finally, part 6 presents the conclusion.
Literature Review
Electrical energy plays an indispensable role in the increasing welfare and economic development of the countries. Because of its specific feature, i.e., maintain the instant balance of the market and lack of high volume storage capacity, this energy carrier is distinct from other carriers. Due to the high costs imposed by power outage, the secure supply of electricity is among the high goals of managers of this industry. Therefore, the mechanism and the controlling factors of this market should be regulated in a way that it leads to the enhanced efficiency, production, and optimum demand.4
The aim of private sector is to achieve highest profit, whereas the government is determined to obtain social benefits. In this regard, the prices reflecting the social benefits and costs are considered, rather than the market prices. These prices are defined as shadow prices in the economy.26 According to this definition, the shadow prices should be used instead of the actual market prices. Obviously, the shadow price is controlled by its limitation. Besides, the shadow prices should be the social benefit produced by the positive project.21
The prefect competition market creates conditions under which the balanced market price is equal to the social price of the given product or service. If the conditions of perfect competition market do not exist for the product or service, the price-based optimum resource allocation would not be realized and the market prices would not be the indicator of actual price of the products and services. An example for this situation is the electricity market. Under these condition, the shadow prices are used for estimation of the actual prices, so that have a proper planning along the investments and the partial development.6 Due to the factors such as restrictions, governmental interventions, and lack of well-organized markets, creation of perfect conditions and full employment seems to be rather difficult in Iran’s economy. This fact is another emphasis on the importance of shadow prices.
Generally, various methods are applied in works conducted on electricity pricing. Some studies forecast electricity price using the time series,7,13,15,16,17,18,20 while some other predict the overall prices and performance of the electricity market.19,22,24,27,29 To forecast this prices, some works conducted using the time series apply structural models such as GARCH, which assumes the variance levels in the future are the same as the ones in the past. GARCH method has been utilized by many researchers.28 Table 1 summarizes the tools used for electricity price forecast using different classifications. As shown in the table, there are two general methods for prediction of this price: time series and structural methods. The time series method uses the statistical approaches for estimation of electricity price using the past records, while the structural method forecasts the prices based on the data processing mechanisms using the present data.
![Table 1: Categorization of Existing Electricity Price Forecasting Tools Ref:[14]](http://www.cwejournal.org/wp-content/uploads/2015/04/Vol10_No1_Deter_Baha_T1-150x150.jpg) |
Table 1: Categorization of Existing Electricity Price Forecasting Tools Ref.14 Click here to View table |
Other time series models have been also used in some other works. For instance, Contreras et al (2003) applied ARIMA for modeling the next-day electricity price.20 In this work, they first applied the logarithmic transfer function and predict electricity price for each season considering the normality of the residuals. Garsia et al (2005) applied GARCH model as a more efficient model for the day-ahead electricity price estimation.28 Ni and Luh (2001) applied Bayesian-based and auto regressive methods for electricity price forecasting. Through this work, they used the past probabilities as the probability distribution function and reported that the model provides efficient forecasting results and can properly show the sudden price changes.12
Furthermore, Bunn (2000) explains that the structural forecasting models are of critical role in the electricity supply market.10 He believes that likewise the artificial neural networks (ANNs) applied for demand estimation; the simulation models can also be used for demand sectors. Centeno et al (2007) applied a structural model for price forecast of companies with middle-term strategies.11 To this aim, they studied market balance problem based on the given conditions to solve it using the optimization problem. Jorge et al (2012) presented a mixed integer nonlinear programming (MILP) for optimization of electricity generation from plants with coal fuel considering the carbon management which minimizes the electricity cost for the given CO2 price in the market23 Chang et al (2013) studied power generation and cross-border grid planning for the integrated ASEAN electricity market using a dynamic linear programming model. The power grid which allows cross-border power transaction can potentially provide some solutions for cost economization. Their study presents the dynamic linear programming model and simulated the optimum development paths of the power generation capacities.31
Sherzod (2013) investigated the induced organizational volatility and regulation modifications affected by the dynamic of daily power prices in wholesale electricity of England and Wales within 1990 to 2001. In this study, he estimated the electricity price volatilities which are relatively dependent on demand.30
Also in Iran, some studies were conducted for electricity price estimation. For example, using the data panel economy measure, the generalized couple method, and auto regressive estimations Bayat (2009) allowed the variation of parameters and estimation of price elasticity for the studied intervals. Then, by providing the dynamicity conditions, she compared the average optimum hourly price trend with the trend of prices obtained from the present static methods and tested the research assumption, which is the difference between the dynamic and static prices.1 Moulaei et al (2012) estimated the electricity price once the market exits from the balance condition. After designing the power market in the form of a systematic dynamic model, the optimum demand, supply, and price values were determined using the optimization model.5
Electricity Model of Iran
The structure designed for electricity market of Iran is shown in Fig. 1. The next-day market electricity generation model of Iran is identified by the relationship between the electricity suppliers and electricity market. By implementation of this model the economic Layout of power generation is realized in Iran Power Grid Management Company (IGMC).
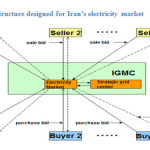 |
Figure 1: The structure designed for Iran’s electricity market. Click here to View figure |
The Model for Determining the Setup of Next-Day Electricity Generation Market of Iran
The main goal pursued by defining this instruction is to determine the requirements and conditions for determining the market winners in the next day and offering the optimum next-day generation Layout by the IGMC.
Target Function of “Economic Generation Layout”
Eq. (2) indicates the “economic generation Layout” in the market:
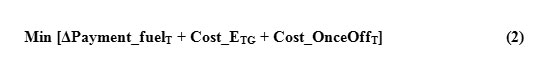
Where, ΔPayment_fuelT is the payment difference for the total fuel of all units of the grid; Cost_ETG: is the total payment costs of the energy for all units of the grid; and Cost_On OffT is the total power on/off costs of the generation units. In Eq. (2), the payment difference of the total fuel of the power units is estimated using the “efficacy of fuel price difference for determination of next-day generation Layout” approach: The energy payment cost for the total units of the grid is estimated using Eq. (3).
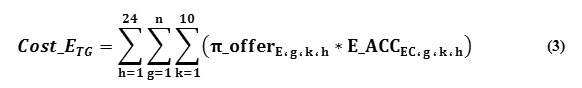
Where,π_offer E.g.k.h is the proposed energy price of unit g in kth step at hth hour. Moreover, power on/off cost of the generation units is estimated using Eq. (4):
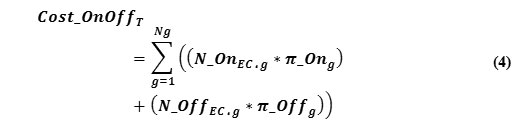
Where, N_On EG.g is the number of power on in unit gth in “economic generation Layout”; N_Off EG.g is the number of power off of unit gth in “economic generation Layout”; π_Ong is the proposed price of gth unit about unit power on; and π_Offg is the proposed cost of gth unit about unit power off.
Output of “Economic Generation Layout”
Eq. (5) expresses the output of economic generation Layout:
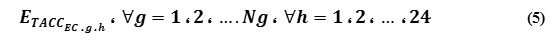
Where, ETACCEC.g.n is the energy received in unit g at hth hour in the economic generation Layout. In other words, the economic generation Layout of Iran electricity market of Iran is a linear programming consisting of the above-described target model, which is indeed the same cost function of the grid for purchasing power from the all plant units. The limitations of this model are summarized as: production potential of the units per each hour; capacity and price steps; the initial energy status of the unit; the maximum daily producible energy; the amount of mutual commitments; power on/off costs of the unit; the latest status of the generation units; forecasting the transmissible capacity of the generation units; “obligatorily in circuit” units; the generation level of the industrial (huge) unit; the amount of cross-border transactions; the balance between the Bus; and the maintenance program of the units.
Method
Linear programming technique is among the tools through which it is possible to select a choice with maximum efficiency among several options.2,8 One of the main characteristics of the linear programming is that solving each counterpart of the initial model provides shadow values. The shadow value is the ultimate value defined as the payment/delivery tendency of a given unit or the entire electricity sector. The shadow value, mentioned as “shadow price” from now on, is different from the actual market price. According to the theory of neoclassical economists, the consumption efficiency of power or any other product or service is fulfilled if its ultimate value or the shadow price equals with the market price. In this regard, the shadow price can be applied as a criterion for social efficiency of the electricity and optimum resource allocation at large scales.8 In linear programming, shadow price is considered as the value of one extra unit of each generation agent, providing the other conditions are constant.6 As previously discussed, a wide range of optimization problems can be solved using the linear programming. However, due to the nature of system under study, for many scientific problems, the coefficients and variables of the target function and constraints cannot be practically considered as the explicit certain accurate numbers. Thus, use of a fuzzy linear programming seems to be inevitable. The most common form of a fuzzy linear programming model for a maximization problem can be expressed as follows25:
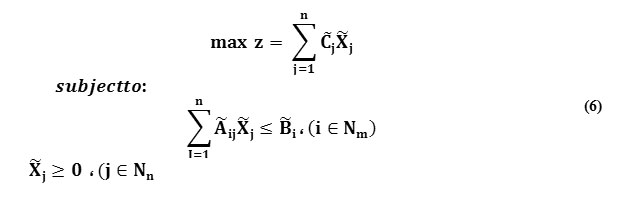
Where,Ãij, Β˜i , and are fuzzy numbers and X˜ij are the parameters presented as fuzzy numbers. To solve fuzzy linear programming problems, they are typically converted to the classic linear or nonlinear problems and then are solved using the existing standard methods such as simplex. There is large number of algorithms for solving the fuzzy linear programming problems proposed by different researchers. Choosing the algorithm is controlled by the fact that which information of the research uncertain is. For the linear fuzzy programming model proposed in this work, the data with uncertainty were entered to the model using the fuzzy linear programming technique. The algorithm used in this part is known as symmetric method, defined based on the Bellman-Zadeh principle, which is more efficient and accurate as compared to other methods.
Model Components and Results Components
Considering the model size and comprehension for the entire country and presence of at least 1,200 Buses in the power grid, the information of the estimations is huge and cannot be introduced in detail. The days selected for model run are based on the electricity consumption volatility during the year, as the volatility in consumption and demand is the most important factor affecting the optimum price. The days selected for this study are as follows:
Fifth of Bahman (January 23), as a day resembling to the average consumption in winter;
Ninth of Tir (June 30), as day with maximum resemblance with the average consumption in summer. Model 1, which belongs to January 23, involves 5,360 decision variables, whereas model 2 consists of 5,420 decision variables and belongs to June 30. The decision coefficients of the target function are the proposed prices of the planet units, which are previously clarified. As a result, the target function would be non-fuzzy. The coefficients of decision variables would be all 1 for the constraints. The right hand of constraints, which explain the generation capacity and potentials of each plant unit, are predictive; as no supplier can be certainly ensured of lack of any next-day problem for power generation in his/her plant as a result, it is possible that the realized generation is less or greater than the amount he/she predicted in the previous day. Based on the comments of experts in power market, the mean prediction error in generation potential of the plants is 0.1 to 16% within a one year period. Note that, this part is explained in the fuzzy from considering the involved uncertainty. The right hand of the other constraint, i.e., electricity market balance, represents the total electricity demand. Since these data are also predictive, they were also converted to fuzzy digits. Based on the comments of experts in this area, during the recent years this value has been varying between 0.0003 to 41% with an average 2.5% prediction error. Once the right hand of constraint has fuzzy values, to obtain the optimum values and model running each fuzzy constraint is converted to three constraints. In this way, the fuzzy linear programming model indeed is converted to the linear programming model, except the number fuzzy constraints of the new fuzzy model becomes three times larger.3
The Results of Fuzzy Linear Programming
In this research, two models were developed for two distinct hours, where the outputs are summarized as the following table.
Table 2: The summary of optimum results of fuzzy linear programming model
| Model No. | Date | Optimum amount of target function (the cost paid by power grid for power purchase in IRR) | Optimum amount of decision making parameters (the energy delivered to each unit in kth step in megawatt) |
| 1 | At 4:00 a.m. of January 25 | 1,643,800,000 | X1=0،،X12=0،،X5309=0.16 |
| 2 | At 16:00of June 30 | 1,303,000,000 | X1=0،،X12=21،،X5362=.62 |
| Reference: Research findings | |||
Table 3: Shadow price values of the fuzzy linear programming
| Model No. | Date | Shadow price of electricity (IRR/KW.h) |
| 1 | At 4:00 a.m. of January 25 | 383 |
| 2 | At 16:00of June 30 | 343 |
The values presented in the Table 3, which are known as shadow prices, represent the importance and efficacy of each constraint in the target function. The shadow price of electricity for Tir 9 (June 30) at 16:00 is 343 IRR per kilowatts, while it is 383 IRRs per kilowatts for (Bahman 5) January 25 at 4:00 a.m. For models in which 530 out of 1200 buses participate in power generation, despite all complications in bus layout, excessive number of decision making factors and the constraints, considerably high demand, and the wide range of consumers varying from domestic to commercial, industrial, agriculture, etc. groups, (which amounts to millions), sine the power grid is integrated, the mentioned groups is faced with a constraint: instant balance of the electricity market. In other words, considering the integrity of overall power grid, the balance between supply and demand in the entire grid can be concurrently realized. Hence, this enormous set of consumers and suppliers is considered as only one constraint for the model. Therefore, only one value is reported for the shadow price corresponding to the instant balance constraints of the market. It is worth to mention that this shadow price is only for a certain hour, while by estimation of day-long shadow price, different shadow prices are obtained for every given hour.
Conclusion
When the power grid is not market-oriented, detecting the real electricity price is not an easy task. Here, the role of shadow prices becomes crucial. The more a given system is price-based unit commitment (PBUC) and the planning is on basis of PBUC, the prices are more clear and fixed, while the systems on basis of security constrained unit commitment (SCUC) and not price-based, the importance of shadow prices becomes higher. Decisions in Iran are made on basis of SCUC, which is not become close to the PBUC planning. This fact indicates the importance of shadow price estimation and having its full details. Through running the model in the deterministic state and comparing its outputs with fuzzy state, it was revealed that the fuzzy model indicates better optimum values when working on fuzzy sate as compared to the deterministic state. This observation can be attributed to the fact that despite the electricity demand of the entire country is met, it does not offer lower costs for the overall power grid of Iran.
References
- J. Conejo, M. A. Plazas, R. Espinola, and A. B.Molina, Day-Ahead Electricity Price Forecasting Using the Wavelet Transform and ARIMA Models, IEEE Transactions on Power Systems, Vol. 20, No.2, pp. 1035-1042, May 2005.
- Khademvatani, D.V. Gordon., 2013. A marginal measure of energy efficiency: The shadow value, Energy Economics 38, 153–159.
- Bellman،E.، and L.A.Zadeh، 1970.Decision-making in a fuzzy environment، Management Science، vol. 17. Pp. B141-B164.
- W. Bunn, Forecasting Loads and Prices in Competitive Power Markets, Proceedings of the IEEE, Vol. 88 No. 2, 2000, pp. 163-169.
- Centeno, J. Reneses, and J. Barquín, Strategic Analysis of Electricity Markets Under Uncertainty: A Conjectured-Price-Response Approach, IEEE Transactions on Power Systems, Vol.22, No. 1, February 2007.
- Ni and P. B. Luh, Forecasting Power Market Clearing Price and Its Discrete PDF Using a Bayesian-based Classification Method, IEEE Power Engineering Society Winter Meeting, Vol. 3, pp.1518–1523, Columbus, OH, 2001.
- J. Nogales, J. Contreras, A. J. Conejo, and R. Espínola, Forecasting Next-Day Electricity Prices by Time Series Models, IEEE Transactions on Power Systems, Vol. 17, No. 2, pp. 342-348, May 2002.
- Forecasting Prices and Congestion for Transmission Grid Operation, EPRC Project Interim Report 4/4/08 – Funding Start Date August 2007, http://www.econ.iastate.edu/tesfatsi/EPRCForecastGroup.htm
- Li, C. C. Liu, J. Lawarrée, M. Gallanti, and A. Venturini, State-of-the-art of electricity price forecasting, Proceedings of 2nd CIGRE/IEEE PES International Symposium, San Antonio, Texas, pp. 110-119, Oct 5-7, 2005.
- Li, C.C. Liu and H. Salazar, Forecasting transmission congestion using day-ahead shadow prices, Proceedings, PSCE, pp. 1705-1709, 2006.
- Li, Electricity price forecasting in a grid environment, Ph.D. Dissertation, University of Washington, Seattle, 2006.
- Li, C. C. Liu, C. Mattson, and J. Lawarrée, Day-ahead electricity price forecasting in a grid environment, IEEE Transactions on Power Systems, vol. 22, no. 1, pp. 266-274, Feb 2007.
- Li, J. Sun, and L. Tesfatsion, Dynamic LMP response under alternative price-cap and pricesensitive demand scenarios, Proceedings, IEEE Power Engineering Society General Meeting, Pittsburgh, PA, July 2008, to appear.
- Contreras, R. Espinola, F. J. Nogales, and A. J. Conejo, ARIMA models to predict next-day electricity prices, IEEE Tran. on Power Systems, Vol. 18, No. 3, pp. 1014-1020, Aug. 2003.
- Eatwell، M.Milgate and P. Newman، 1987.The New Palgrave: a Dictionary of Economics،The Macmillan Press Limited، vol. 4، Q to Z،pp. 316-317.
- Nicolaisen, V. Petrov, and L. Tesfatsion, Market power and efficiency in a computational electricity market with discriminatory double-auction pricing, IEEE Transactions on Evolutionary Computation, Vol. 5, No. 5, pp. 504-523, October 2001.
- Jorge Cristo´ balØŒ GonzaloGuille´n-Gosa´ lbezØŒLaureanoJime´nezØŒAngelIrabien.ØŒ2012. MINLP model for optimizing electricity production from coal-fired power plants considering carbon managementØŒ energy policy 51ØŒpp 493-501.
- Sun and L. Tesfatsion, `Dynamic testing of wholesale power market designs: An open-source agent-based framework, Computational Economics, Vol.30, pp. 291-327, 2007.
- Lai، Y-J.، and C-L. Hwang،Fuzzy mathematical programming: methods and applications، Springer-Verlag.
- Little،M.D. and Mirrlees، J.A.، 1974. Project Appraisal and Plonning for Developing Countries، London: Heinemann.
- Yu, C.C. Liu, and L. Tesfatsion, Modeling of suppliers’ learning behaviors in electricity market environment, Proceedings of the 14th International Conference on Intelligent System Applications to Power Systems (ISAP2007), Kaohsiung, Taiwan, November 4-8, 2007. Accepted for the International Journal of Engineering Intelligent Systems.
- C. Garcia, J. Contreras, J., M. van Akkeren, and J. B. C. Garcia, A GARCH forecasting model to predict day-ahead electricity prices, IEEE Transactions on Power Systems, Vol. 20, Issue 2, pp. 867-874, May 2005.
- E. Widergren, J. Sun, and L. Tesfatsion, Market Design Test Environments, Proceedings, IEEE Power Engineering Society General Meeting, Montreal, June, 2006.
- Sherzod N. Tashpulatov.،Estimating the volatility of electricity prices: The case of the England and Wales wholesale electricity market، energy policy 60،pp 81-90.
- Youngho Chang، Yanfei Li.، 2013.Power generation and cross-border grid planning for the integrated ASEAN electricity market: A dynamic linear programming model، Energy Strategy Reviews 2،pp 153-160.






